 Avoiding the Misinformed
Avoiding the Misinformed
Programmers often spend more time un-doing bad information than using good information. One of the comments that set me off recently was someone “explaining” to others on a blog why PHP was not an object oriented language. Then he continued to blather on about the difference between compiled and interpreted languages. Whether or not a language is compiled or not has nothing to do with whether or not it is an object oriented language. Having interfaces, classes and communication between objects are the key criteria of an OOP language, and certainly since PHP5 has been a full-fledged OOP language. (We PHPers should not feel singled out because I recently saw post where a Java programmer pronounced that neither Python nor Perl were OOP, and she was “informed” otherwise by irate Python programmers. Perl has been OOP since V5.) So here I am again wasting time grumbling about people who don’t know what they’re talking about.
Instead of frothing at the mouth over the misinformed, I decided to spent more time with the well-informed. To renew my acquaintance with algorithms I began reading Algorithms 4th Ed. (2011) by Sedgewick and Wayne. Quickly, I learned some very basic truths about algorithms that had been only vaguely floating around in my head. First and foremost are the following:
Bad programmers worry about the code.
Good programmers worry about data structures and their relationships.
—Linus Torvalds (Creator of Linux)
Since we’ve been spending time on this blog acting like good programmers, that was reassuring. In this post, I’d like to look at two things that are important for developing algorithms: 1) What to count as a “cost” in developing algorithms, and 2) Identifying good and bad algorithmic models. First, though, play and download the example. Using two different algorithms, a logarithmic and a linear (both pretty good ones), I’ve added “dots” to loop iterations to visually demonstrate the difference between a logarithmic algorithm (binary search) and a linear algorithm (loop). The “expense” of the algorithm can be seen in the number of dots generated.
![]()
![]()
The example is a pretty simple one. However, since this blog is about PHP Design Patterns, I added a little Factory Method. The two algorithm classes act like clients making requests through the factory for a big string array with over 1,000 first names. Figure 1 shows the file diagram:
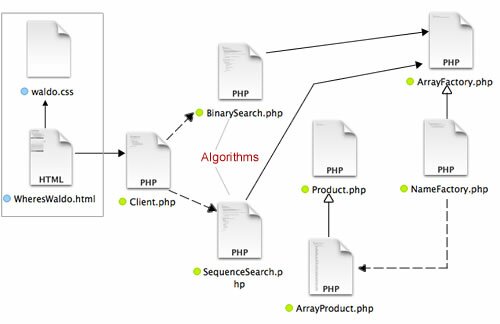
Figure 1: File diagram for use of Factory Method by two algorithm clients.
In looking at the file diagram, you may be thinking, “Why didn’t you use a Strategy pattern coupled with that Factory Method?” I thought about it, but then decided you could do it yourself. (Why should I have all the fun?)
Lesson 1: Leave the Bag of Pennies
The first lesson I learned in Bank Robbery 101 was to leave the bag of pennies. They’re just not worth it. Speed is everything in a bank robbery, and so you pay attention to how to get the most with the least time. The same thing applies to analyzing algorithms. For example, an object (as compared to an integer, boolean or string) has an overhead of 16 bytes. I have actually seen posts intoning, “objects are expensive…” Just to be clear,
Objects are not expensive. Iterations are expensive, quadratic algorithms are expensive.
In evaluating an algorithm you need to see how many operations must be completed or the size and nature of the N. An N made of up strings is different than an N made up of Booleans or integers. A quadratic (N²) and cubic (N³) algorithm are among the worst. They’re gobbling up kilo- or megabytes, and so that 16 bytes seems pretty silly to worry about. So instead of seeing an algorithm weight expressed as N² + 84 bytes, you’ll just see it expressed as ~N². (When you see a ~ (tilde) in an algorithm, it denotes ‘approximately.’) Another way of understanding the ~ is to note, They left the bag of pennies.
Lesson 2: Watch out for Nested Loops; they’re Quadratic!
I’ve never liked nested loops, and while I admit that I’ve used them before, I just didn’t like them. They were hard to unwind and refactor, and they always seemed to put a hiccup in the run-time. Now I know why I don’t like them; they’re quadratic.
Quadratic algorithms have the following feature: When the N doubles, the running time increases fourfold.
An easy way to understand the problem with quadradics is to consider a simple matrix or table. Suppose you start with a table of 5 rows and 5 columns. You would create 5² cells—25 cells. Now if you double the number to 10, 10² cells = 100. That’s 4 x 25. Double that 10 to 20 and your have 20² or 400. A nested loop has that same quality as your N increases. If both your inner and outer loop N increases, you’re heading for a massive slowdown.
Algorithms, OOP and Design Patterns are Mutually Exclusive
An important fact to remember is that good algorithms do not guarantee good OOP. Likewise, good OOP does not mean good algorithms. Good algorithms make your code execute more efficiently and effectively. Good OOP makes your programs easier to reuse, update, share and change. Using them together is the ultimate goal of a great program.
 A few years ago I created a post on Skip Lists (different blog), and several people told me that it clarified the concept of skip lists for them; so I’m reproducing it here for PHP developers. Using the analogy of rail travel in the New York-Hartford-Boston area, I show how the skip list can work in the world apart from programming. Living in Bloomfield, Connecticut, I’m about halfway between Boston and New York City. Lately they’ve been talking about building a high speed rail to Hartford and on to Springfield, Massachusetts. Naturally, when thinking about such a rail system, I like to think that the really fast part of the trip would be between New York City, Hartford, and Boston. Of course they’d need an express to stop off in New Haven and Springfield. Further, lots of other towns, including Bloomfield, would need some kind of local line. Left to my own devices, I would build the following lines:
A few years ago I created a post on Skip Lists (different blog), and several people told me that it clarified the concept of skip lists for them; so I’m reproducing it here for PHP developers. Using the analogy of rail travel in the New York-Hartford-Boston area, I show how the skip list can work in the world apart from programming. Living in Bloomfield, Connecticut, I’m about halfway between Boston and New York City. Lately they’ve been talking about building a high speed rail to Hartford and on to Springfield, Massachusetts. Naturally, when thinking about such a rail system, I like to think that the really fast part of the trip would be between New York City, Hartford, and Boston. Of course they’d need an express to stop off in New Haven and Springfield. Further, lots of other towns, including Bloomfield, would need some kind of local line. Left to my own devices, I would build the following lines:
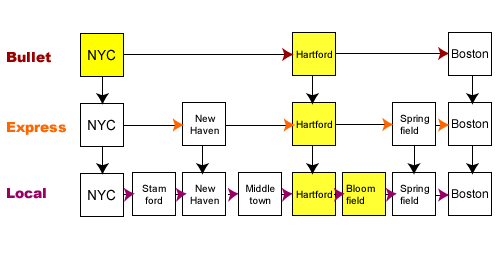
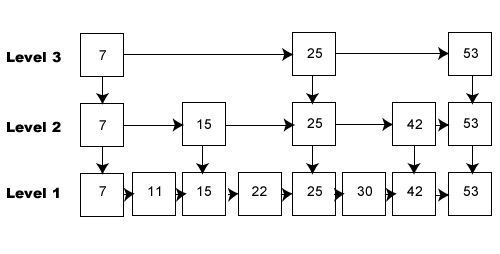
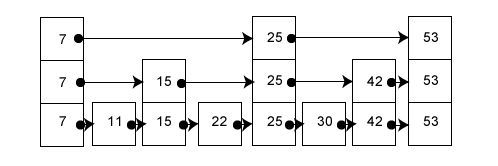
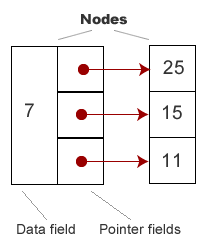 Figure 5: Node with multiple pointers
Figure 5: Node with multiple pointers List Searches
List Searches To get a sense of how the binary search works, take a piece of paper (a discarded joke-a-day calendar page works well) and fold it into two equal halves. Keep folding it in half until you have 6 folds. After six folds I could not get a seventh fold—the paper was too fat by that point.
To get a sense of how the binary search works, take a piece of paper (a discarded joke-a-day calendar page works well) and fold it into two equal halves. Keep folding it in half until you have 6 folds. After six folds I could not get a seventh fold—the paper was too fat by that point.
Recent Comments