 A few years ago I created a post on Skip Lists (different blog), and several people told me that it clarified the concept of skip lists for them; so I’m reproducing it here for PHP developers. Using the analogy of rail travel in the New York-Hartford-Boston area, I show how the skip list can work in the world apart from programming. Living in Bloomfield, Connecticut, I’m about halfway between Boston and New York City. Lately they’ve been talking about building a high speed rail to Hartford and on to Springfield, Massachusetts. Naturally, when thinking about such a rail system, I like to think that the really fast part of the trip would be between New York City, Hartford, and Boston. Of course they’d need an express to stop off in New Haven and Springfield. Further, lots of other towns, including Bloomfield, would need some kind of local line. Left to my own devices, I would build the following lines:
A few years ago I created a post on Skip Lists (different blog), and several people told me that it clarified the concept of skip lists for them; so I’m reproducing it here for PHP developers. Using the analogy of rail travel in the New York-Hartford-Boston area, I show how the skip list can work in the world apart from programming. Living in Bloomfield, Connecticut, I’m about halfway between Boston and New York City. Lately they’ve been talking about building a high speed rail to Hartford and on to Springfield, Massachusetts. Naturally, when thinking about such a rail system, I like to think that the really fast part of the trip would be between New York City, Hartford, and Boston. Of course they’d need an express to stop off in New Haven and Springfield. Further, lots of other towns, including Bloomfield, would need some kind of local line. Left to my own devices, I would build the following lines:
Bullet
- New York
- Hartford
- Boston
Express
- New York
- New Haven
- Hartford
- Springfield
- Boston
Local
- New York
- Stamford
- New Haven
- Middletown
- Hartford
- Bloomfield
- Springfield
- Boston
Given these choices, I know that I can easily get to Bloomfield by taking the Local at Grand Central Terminal in New York City. However, I’d really like to skip stops in Stamford, New Haven and Middletown. If I took the express, I’d have a stop in New Haven and then on to Hartford where I could get on the Local to Bloomfield. That would be faster, but it would not be the fastest route.
To determine the fastest route, assuming that I have to go in the same direction and cannot backtrack, I diagramed the three lines in Figure 1.

Figure 1: Three train lines between NYC and Boston
Looking at Figure 1, it is not too difficult to determine the quickest route between NYC and Bloomfield.
The route that skips the most stops is the quickest route.
Trace your finger from NYC to Bloomfield in Figure 1 and you can determine that route. To see if you found it, look at Figure 2 to see the fastest route highlighted in yellow.
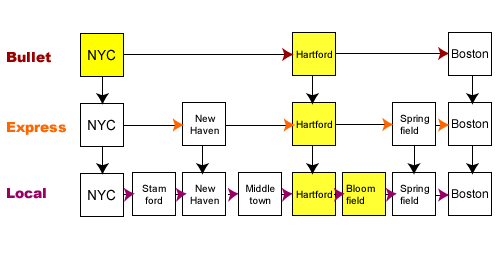
Figure 2: The Route that Skips the Most Stops
If you traced the route highlighted in yellow in Figure 2; then you understand how skip lists work. In a similar way, the Binary Search discussed here does not start at the beginning and iterate through an entire ordered list. Rather it splits the list determining the quickest way to the search item.
From Train Lines to Linked Lists
To go to the next step, you need to understand Linked Lists which we discussed in a recent post. What I’d like to do is to transform our train lines into a linked list. The first step is to change the different towns on the lines to nodes in a linked list. Figure 3 shows the first step in this transformation:
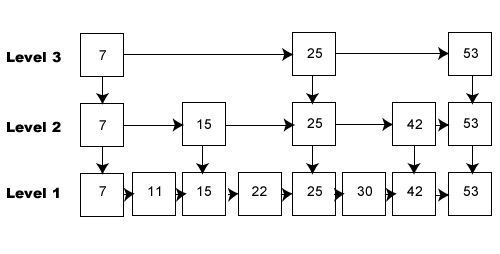
Figure 3: From Train Stops to Nodes in a Linked List
My hunch is that if I asked you what was the quickest route to find the value “30” you’d know just what to do. However, the diagram still looks like a train dispatcher’s chart, and so we’ll update it a bit to look more like a linked list. Figure 4 shows this new diagram.
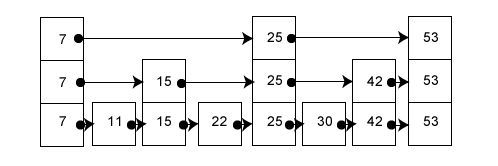
Figure 4: Linked list with multiple pointers<[/caption] 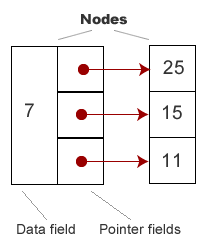 Figure 5: Node with multiple pointers
Figure 5: Node with multiple pointers
Keeping in mind that the linked lists are ordered (sorted) our search for the value “30” would look something like this:
- Starting point would be on the shortest linked list: 30 is > 25 but < 53.
- Drop to next level down to the second shortest list: 30 is < 43.
- Drop to next level down to the third shortest list: 30 == 30. Your search is over.
Now we’re ready to deal with coding skip lists in PHP5. We’ll have to work out the algorithms, and in the next post on skip lists we should be able to have a working skip list that we can use with an iterator pattern.
Copyright © 2014 William Sanders. All Rights Reserved.
0 Responses to “PHP Skip Lists 1: The Quickest Route Home”